前回平均値-範囲法のGR&Rの解析方法を説明した。しかしこれはエクセルがなかった時代に簡易的に計算する方法として用いられていた手法である。現代であれば分散分析表からGR&Rを計算するほうがよい。
ということで今回はANOVA法を用いた解析方法について解説する。
実際にはほぼ二元配置分散分析と同様なので、詳細な考え方はこちらを見てください。
使用するデータ
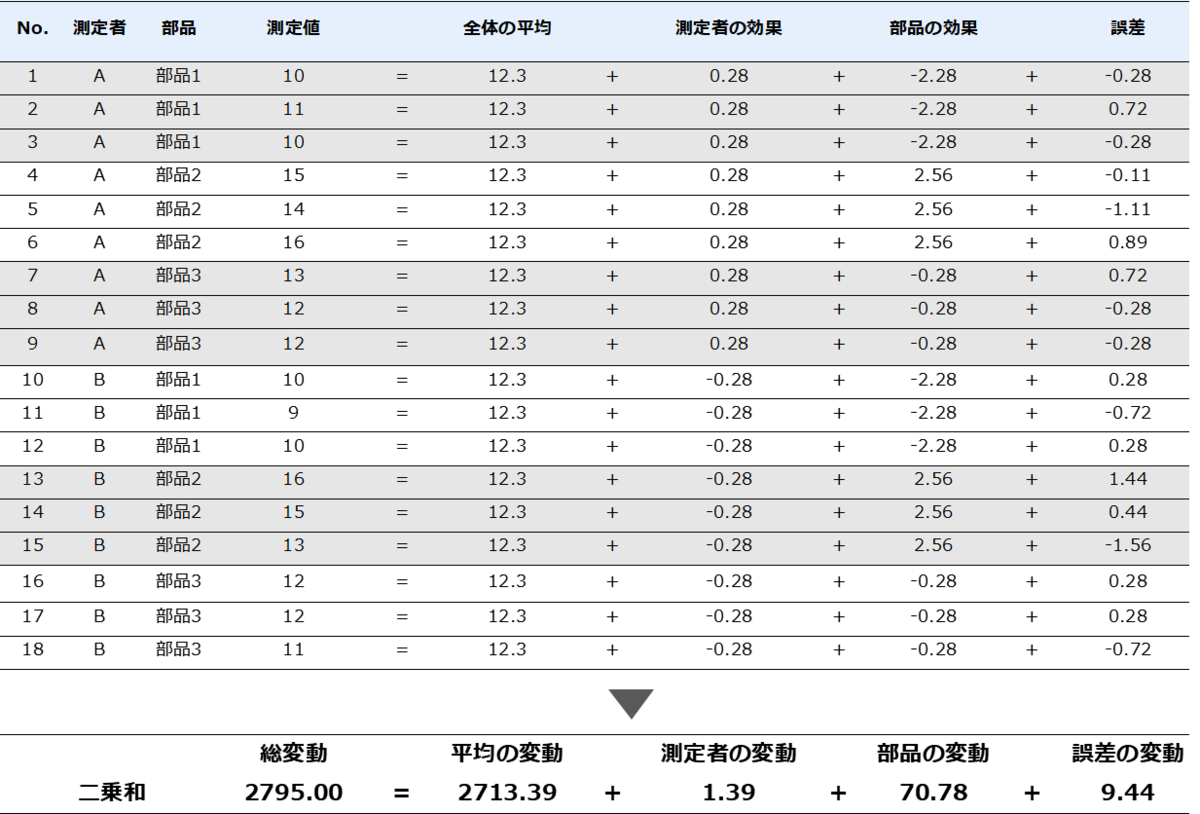
今回はGR&Rを行うデータとして、下記のデータを使用する

測定者:二人(Aさん、Bさん)
部品数:3個
繰り返し数:3回
各因子の効果を求める
まずは人ごとと、部品ごとの平均値を算出し、それを全体の平均値との差分を取ることで、それぞれの効果を求める。

これを行うことにより各データを
と分解することが出来る。
各因子の変動を求める
それぞれの効果の二乗和を取り、変動を計算する。
各因子の自由度を求める
続いてそれぞれの自由度を求める
分散分析表を作る
これまでのデータから平方平均=二乗和/自由度を計算して、以下の分散分析表を作る。


さて、それぞれ計算した平方平均は、AV,EV,PVを若干変形したものの推定量になっている(らしい。この式を探すのにすごい苦労した)
%GRRを計算する。
分散分析表の一番右にある推定量の式を変形して、AV,EV,PV,GRR,TVを計算していく。
ちなみに、測定誤差が大きく、が大きすぎると、
や
は計算上0以下になり得る。そうなると平方根で虚数が出てきて後の計算が出来ないので、その時は
、
として進めるとよい。
下記の目安に当てはめると、今回の系はNGとなり、精度の改善の余地がある。
<10%:OK
10%~30%:場合によっては許容
>30%:NG
ちなみに平均値-範囲法の%GRR=33.8%に比べてもほぼ同じ値になった。
これでGRRの解説はすべて終わり。結構大変でしたが今まで漫然と使っていて、どんな理論があるのかを多少は勉強できてよかったです。
エクセルのテンプレートまではそのうち作りたいな。
参考サイト
https://evolvingbook.com/wp-content/uploads/2018/12/GRR.pdf
https://msc-conf.com/wp-content/uploads/2016/06/2004-Best-Paper-1.pdf