二元配置分散分析（two-way ANOVA）を自力でやってみる④：分散分析-交互作用編

前回に続き二元配置分散分析（two-way ANOVA）。

f:id:Chemstat:20210425220219p:plain

データの準備

繰り返しのある二元配置分散分析としてこちらのデータを使用する。

要素１：a, b, c

要素２：A, B

f:id:Chemstat:20210402225823j:plain

分散分析（標本・列）

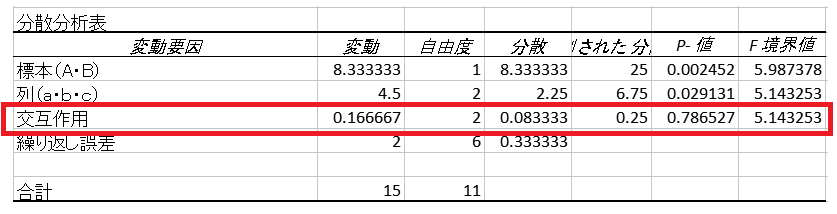
f:id:Chemstat:20210501192606p:plain

今回は交互作用の効果をF検定進めていく。

下記式でいうところの $\gamma$ を求める。

f:id:Chemstat:20210427210643p:plain

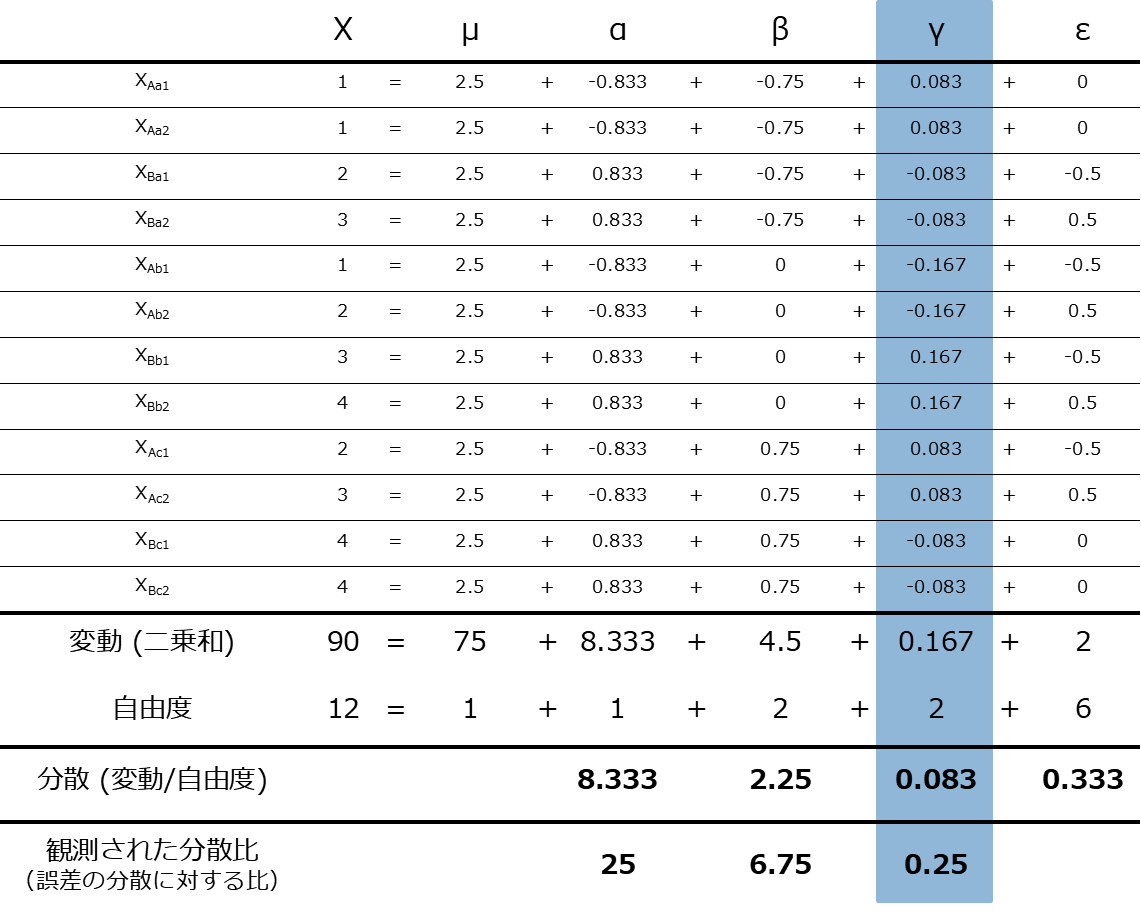
f:id:Chemstat:20210501192704p:plain

交互作用の分散

交互作用を一言でいうと「二つの因子が組み合わさったときに追加で出現する効果」である。ある成分をA→Bに変えた時、もう一方の成分がaかbかで異なる効果が現れる。

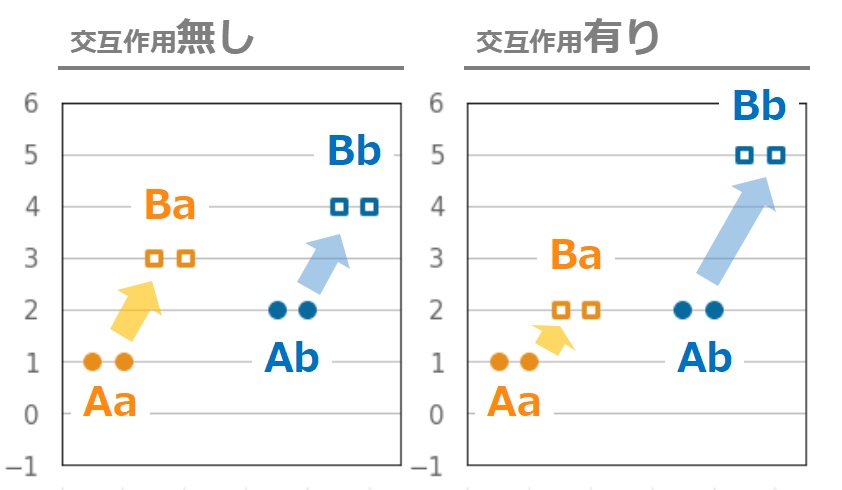
f:id:Chemstat:20210627143612j:plain

分散分析はその過程で各要素の効果を求めることになる。平均値に単純にそれぞれの効果を足した値と、実際のデータのずれが交互作用と言える。

下図をみてピンとくる方もいるかと思うが、やってることは誤差の計算とほぼ同じである。データ数が各群1の場合だと、誤差と交互作用は分離できなくなってしまうので、交互作用が気になる場合はデータ数を増やして評価する必要がある。

f:id:Chemstat:20210627143731j:plain

ちなみに化学材料の統計分析をやっているとこの交互作用に多分に悩まされることになる。二成分に限らず、三成分・四成分といった複数成分の交互作用も平気で出てくるし、ひとたび交互作用が出てしまうと成分単独の効果が議論しづらくなってしまう。結局交互作用が出づらい実験系を組むしかなくなるケースが多い。なにかおすすめの方法があったら是非教えてほしい。

交互作用の分散

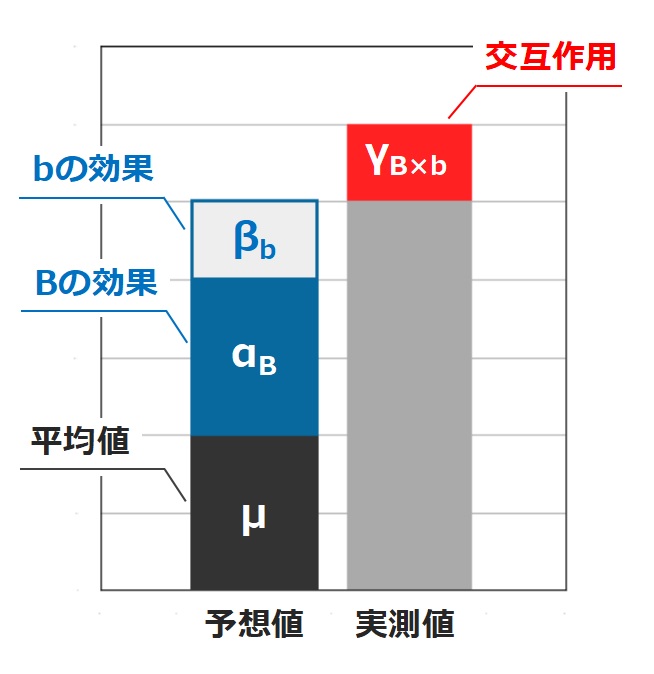
では早速交互作用の項 $\gamma$ を求めていくのだが、計算の仕方は非常に簡単で、各データ群の平均値 $\bar{x}$ と、標本・列の効果から計算される予想値 $\mu+\alpha+\beta$ の差分が交互作用 $\gamma$ に相当する。図にするとこんな感じ。

f:id:Chemstat:20210705213952p:plain

ということで早速計算していこう。数が多いけれどやってることは同じ計算の繰り返しなので適当に読み流してください。計算には前回の記事で計算した値を用いているので、導出が分からなくなったらそちらを見てみてください。

$\gamma_{Aa} =\bar{x}_{Aa} - (\mu_{total} + \alpha_A + \beta_a) =1-(2.5-0.833-0.75)=0.083$

$\gamma_{Ba} =\bar{x}_{Ba} - (\mu_{total} + \alpha_B + \beta_a)=2.5-(2.5+0.833-0.75)=-0.083$

$\gamma_{Ab} =\bar{x}_{Ab} - (\mu_{total} + \alpha_A + \beta_b)=1.5-(2.5-0.833+0)=-0.167$

$\gamma_{Bb} =\bar{x}_{Bb} - (\mu_{total} + \alpha_B + \beta_b) =3.5-(2.5+0.833+0)=0.167$

$\gamma_{Ac} =\bar{x}_{Ac} -(\mu_{total} + \alpha_A + \beta_c) =2.5-(2.5-0.833+0.75)=0.083$

$\gamma_{Bc} =\bar{x}_{Bc} -(\mu_{total} + \alpha_B + \beta_c) =4-(2.5+0.833+0.75)=-0.083$

分散分析を行うため、続いてはこの $\gamma$ の分散を求める。

エクセルではそれぞれの効果の二乗和を「変動」と呼び、それを自由度で割ったものを「分散」と呼んでいる。

変動

$s_{\gamma}^2= {\gamma_{Aa}}^2 \times n_{Aa} + {\gamma_{Ba}}^2 \times n_{Ba}+ {\gamma_{Ab}}^2 \times n_{Ab}+ {\gamma_{Bb}}^2 \times n_{Bb}+ {\gamma_{Ac}}^2 \times n_{Ac}+ {\gamma_{Bc}}^2 \times n_{Bc}$

$\scriptsize=(0.083)^2 \times 2+(-0.083)^2 \times 2+(-0.167)^2 \times 2+(0.167)^2 \times 2+(0.083)^2 \times 2+(-0.083)^2 \times 2\normalsize=0.167$

自由度

$\phi_{\gamma}=\phi_{\alpha}\times\phi_{\beta}=2\times1=2$

分散

$\begin{align*} V_{\gamma} = \frac{s_{\gamma}^2 }{\phi_{\gamma}}\scriptsize =\frac{ 0.167}{2}\normalsize=0.083...\end{align*}$

交互作用のF検定

観測された分散比

これがF値に相当する。

$\begin{align*}F=\frac{ V_{\gamma}}{V_{\varepsilon}}=\frac{0.083...}{0.333...}=0.25\end{align*}$

p値

自由度 $\phi_{\alpha},\phi_{\varepsilon}=2,6$ のF分布において $F=0.25$ の上側の累積確率に相当するので、0.786になる。Excelやpythonで計算してもらえばよい。

F境界値

自由度 $\phi_{\alpha},\phi_{\varepsilon}=2,6$ のF分布において上側の累積確率が5%となるF値なので、5.143...となる。こちらもExcelやpythonで計算してもらえれば。

この分散分析で最終的に得られるF値、p値によってグループ間の差が統計的に有意かを調べることが出来る。ちなみに帰無仮説は「交互作用がすべてゼロ（ $\gamma_{Aa}=\gamma_{Ba}=\gamma_{Bb}=\gamma_{Bb}=\gamma_{Ac}=\gamma_{Bb}=0$ ）」である。今回のF=0.25ではp値は0.786なので、棄却域を0.05で取る場合帰無仮説は棄却され、「交互作用がすべてゼロ」ということになる。