Stanでベイズ推定を使ってモデルを学習させた後に、学習後のモデルを使って新しく予測値とその信頼区間を生成したいと思った。
cmdstanpyを色々と調べたところgenerate_quantitiesという関数が用意されているらしい。
今回は単回帰分析をした後に新たに予測値を生成してみる。

使用するデータ
色んな記事に使っているこのデータを今回も使用することにする。
|
(説明変数) |
1 |
2 |
3 |
4 |
5 |
|
(被説明変数) |
2 |
6 |
6 |
9 |
6 |
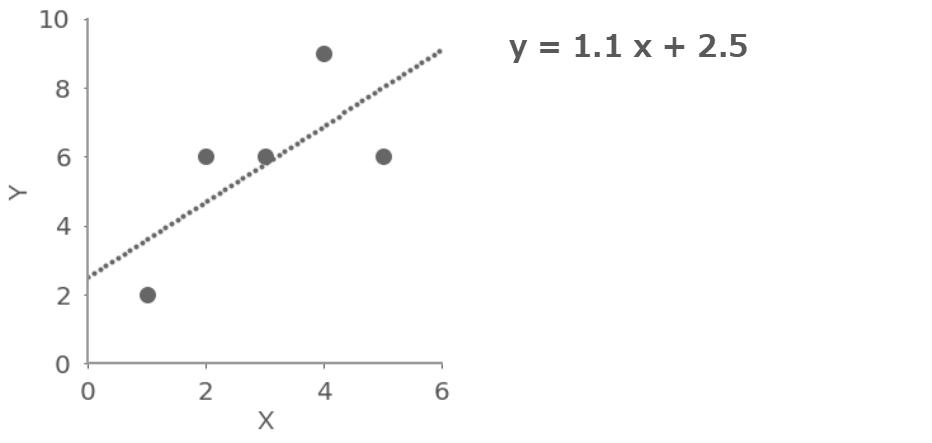
最小二乗法で計算した結果はこちら。
単回帰分析
fitを使って単回帰分析をする方法はこちらの記事にまとめたので、細かい事はこちらを参照頂くとして、コードだけ書いておく。
stanコード
data {
int<lower=0> N;
vector[N] X;
vector[N] Y;
}
parameters {
real a;
real b;
real<lower=0> sigma;
}
model {
Y ~ normal( b*X + a, sigma);
a ~ normal(0,1000);
b ~ normal(0,1000);
sigma ~ normal(0,1000);
}
pythonコード
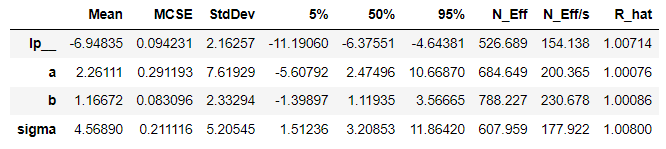
import os import time import numpy as np import arviz as az from matplotlib import pyplot as plt from cmdstanpy import CmdStanModel import pandas as pd #データを作成 x = np.array([1, 2, 3, 4, 5]) y = np.array([2, 6, 6, 9, 6]) stan_file = "./test.stan" exe_file = "./test" #コンパイル if not os.path.exists(exe_file): model = CmdStanModel(stan_file=stan_file) else: model = CmdStanModel(exe_file=exe_file) data = { "N": len(x), "X": x, "Y": y } import multiprocessing num_cpu = multiprocessing.cpu_count() fit = model.sample( data=data, chains=4, # chain数 seed=1, # seed固定 iter_warmup=1000, # warmupの数 iter_sampling=2000, # samplingの数 parallel_chains=num_cpu, # 並列数 save_warmup=True, # warmupもCSVに保存 thin=1, # サンプリング間隔 #output_dir=output_dir, # 出力先 show_console=False, # 標準出力 show_progress=True # progress出力 ) fit.summary()
これを実行するとこんな結果が得られる。
データの予測
ここからは本題のデータの予測について。
generate quatitiesを使うと、先ほど推定したパラメーターの値を使って新たに計算することができる。
推定の段階でstanのコードにgenerated quantitiesのブロックで指定することもできるが、後々計算を追加したくなったときに時間のかかる推定プロセスを省けるメリットがある。
ではまずはStanのコード。
stanコード
data {
int<lower=0> M;//予測をするデータ数
vector[M] X_new;//予測に使う説明変数X
}
parameters {
//学習時に利用したパラメータ
real a;
real b;
real<lower=0> sigma;
}
generated quantities {
//回帰直線の予測値
vector[M] new_Y1;
new_Y1 = b*X_new + a;
//データ点の予測値
vector[M] new_Y2;
for (m in 1: M){
new_Y2[m] = normal_rng( b*X_new[m] + a, sigma);
}
}
今回使用するstanのコードは、data,parameters,generated_quantitiesの三種類で構成されている。
new_Y2の予測は「normal」ではなく、「normal_rng」を使って平均値b*X+a、標準偏差sigmaの正規分布から乱数を生成している。どうもvectorでまとめて指定できないらしく、for文で個別に指定している。

pythonコード
先ほどのstanコードを「test_gen.stan」に保存し、以下のpythonコードを実行すると、データの予測が行われる。データの予測用に「generate_quantities」という関数が用意されており、これを使った。
#予測用のstanコードをmodel_ppcにコンパイルする stan_file = "./test_gen.stan" exe_file = "./test_gen" #コンパイル if not os.path.exists(exe_file): model_ppc = CmdStanModel(stan_file=stan_file) else: model_ppc = CmdStanModel(exe_file=exe_file) #新しく推定に使う説明変数をdata_newに入力 X_new = np.arange(-5,10,1) data_new = { "M": len(X_new), "X_new": X_new, } #generate_quantitiesを利用してモデルから予想されるデータを生成する new_quantities = model_ppc.generate_quantities( data = data_new, #予測用のデータを指定 previous_fit = fit #学習に使用したモデルを指定 )
計算が終わったら、格納されているデータを取り出してみる。
sample_plus = new_quantities.draws_pd(inc_sample=True) print(sample_plus)
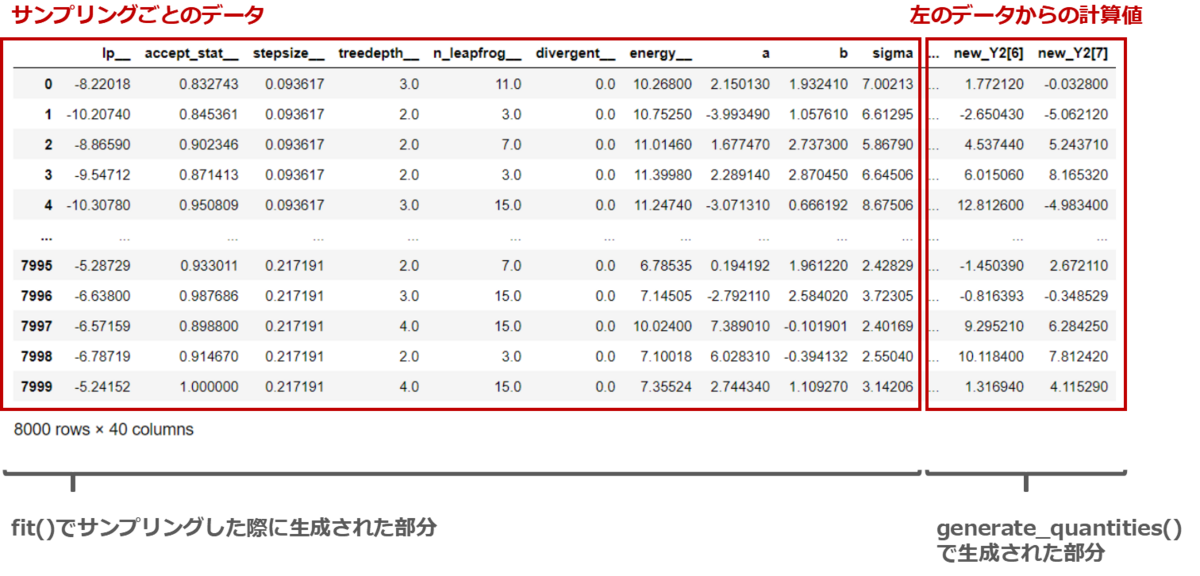
このような表が出力されてくる。もともとmodelにはfit()を実行した際の各サンプリングごとのデータが格納されており、generate_quantiteis()を実行すると、そのデータを使って計算値を返してくれる。
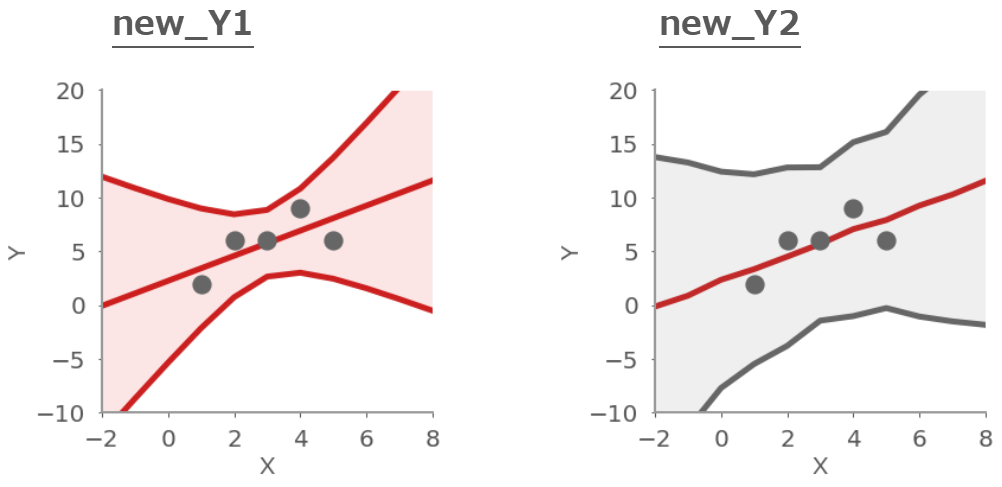
すべてのデータをグラフにするとこんな感じ。データの重心で付近で精度が高くなっているのがわかる。
y_new1 = sample_plus.iloc[:, -len(X_new)*2:-len(X_new)]
y_new2 = sample_plus.iloc[:, -len(X_new):] for n in np.arange(8000): ax1.scatter(X_new, y_new1.iloc[n].values) for n in np.arange(8000): ax1.scatter(X_new, y_new2.iloc[n].values)
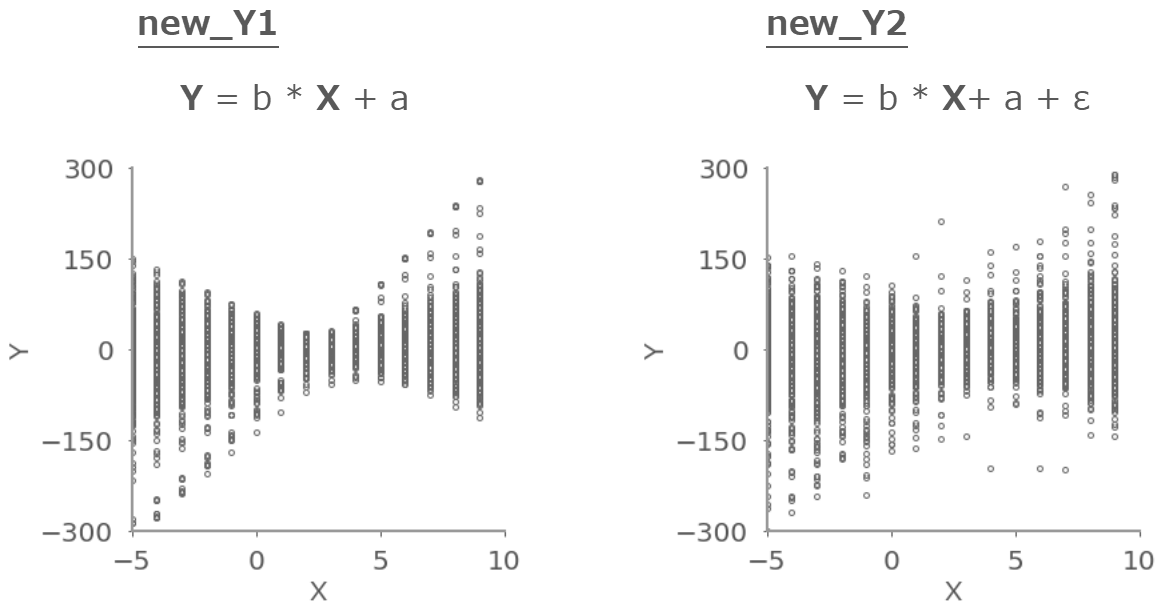
この結果の平均値や標準偏差を計算することで予測値や範囲を得ることができる。
今回は平均値±標準偏差の範囲を予測区間をグラフにした。
#平均と標準偏差を計算して追加する sample_plus.loc['Mean'] = sample_plus.mean() sample_plus.loc['Stds'] = sample_plus.std() #グラフ用のデータを計算 new_Y1_ave = sample_plus.loc['Mean'][-len(X_new)*2:-len(X_new)] new_Y2_ave = sample_plus.loc['Mean'][-len(X_new):] new_Y1_std = sample_plus.loc['Stds'][-len(X_new)*2:-len(X_new)] new_Y2_std = sample_plus.loc['Stds'][-len(X_new):]
plt.scatter(x,y)#元データ plt.plot(X_new, new_Y1_ave)#予測値の平均値 plt.plot(X_new, new_Y1_ave + new_Y1_std)#平均値+標準偏差 plt.plot(X_new, new_Y1_ave - new_Y1_std)#平均値-標準偏差 plt.fill_between(X_new,new_Y1_ave - new_Y1_std, new_Y1_ave + new_Y1_std)#区間の塗りつぶし
plt.scatter(x,y)#元データ plt.plot(X_new, new_Y2_ave)#予測値の平均値 plt.plot(X_new, new_Y2_ave + new_Y2_std)#平均値+標準偏差 plt.plot(X_new, new_Y2_ave - new_Y2_std)#平均値-標準偏差 plt.fill_between(X_new,new_Y2_ave - new_Y2_std, new_Y2_ave + new_Y2_std)#区間の塗りつぶし
参考サイト
Run Generated Quantities — CmdStanPy 0.9.64 documentation