最尤法を使って線形回帰分析をやってみる - 統計を学ぶ化学系技術者の記録

今までいろいろな記事で線形回帰分析の解説をしたが、この時は最小二乗法を用いたものだった。

最尤法を使ってもできるので、今回はその計算を紹介したい。

以下の4ステップに従って進めていく。

①データを集める

まずは使用するデータを決める。

色んな記事に使っているこのデータを今回も使用することにする。

$x$ (説明変数)	1	2	3	4	5
$y$ （被説明変数）	2	6	6	9	6

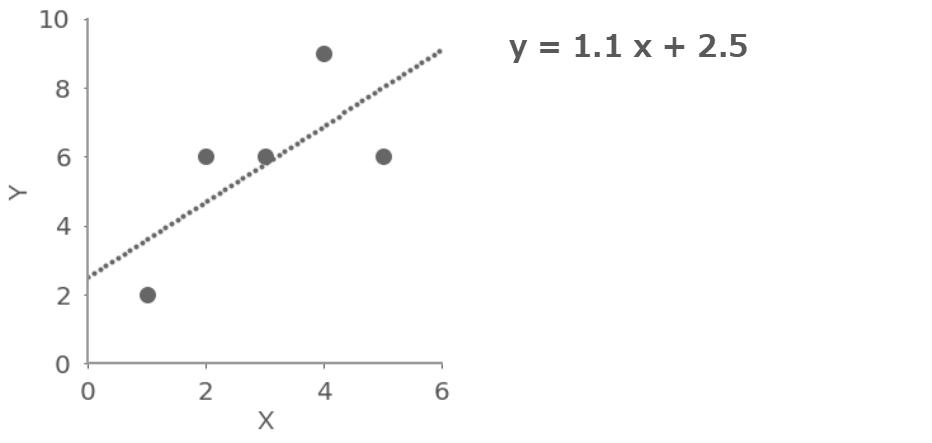
グラフにするとこんな感じ。最小二乗法で求めた回帰直線の値も載せている。これが最尤法でどうなるかを見ていくことにする。

②モデルを作る

モデルを作る、というと大げさに感じるが、決めるべきことは

①xとyの関係式

②誤差の分布

の二つである。今回は線形近似なので

① $y=ax+b$ の単回帰直線で表される

②誤差は回帰直線から分散 $\sigma^2$ の分布を持つ

ということにする。このモデルの自由度が最尤法のいい所だと思っている。

③尤度関数を作る

今回のモデル $y_i=ax_i+b+\varepsilon$ に従うと、それぞれの $y_i$ が誤差の正規分布に従った確率度密度関数に従うことになる。

これにそれぞれの $y_i$ を当てはめると、各データ点の確率密度を求めることが出来る。

ただこの式よく見ると、分布を決めているのは $\varepsilon_i$ だけなので

$\varepsilon_i=y_i-(ax_i+b)$ は全て同じ確率密度関数に従う、と変換することも出来る。

このプロットではすべて同じ確率分布上で示すことが出来るので、やや見やすくなる。

それぞれのデータ点の確率密度はこうなる

$\begin{align*}f(y_i)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{\varepsilon_i^ 2}{2\sigma^ 2}\right)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{(y_i-a{\times}x_i-b)^ 2}{2\sigma^ 2}\right)\end{align*}$

$\begin{align}f(y_1)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{\varepsilon_1^ 2}{2\sigma^ 2}\right)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{(2-a{\times}1-b)^ 2}{2\sigma^ 2}\right)\end{align}$

$\begin{align}f(y_2)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{\varepsilon_2^ 2}{2\sigma^ 2}\right)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{(6-a{\times}2-b)^ 2}{2\sigma^ 2}\right)\end{align}$

$\begin{align}f(y_3)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{\varepsilon_3^ 2}{2\sigma^ 2}\right)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{(6-a{\times}3-b)^ 2}{2\sigma^ 2}\right)\end{align}$

$\begin{align}f(y_4)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{\varepsilon_4^ 2}{2\sigma^ 2}\right)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{(9-a{\times}4-b)^ 2}{2\sigma^ 2}\right)\end{align}$

$\begin{align}f(y_5)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{\varepsilon_5^ 2}{2\sigma^ 2}\right)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{(6-a{\times}5-b)^ 2}{2\sigma^ 2}\right)\end{align}$

これを掛け合わせたものが尤度関数となり、 $a,b,\sigma$ の3つの変数を持った関数になる。

$\begin{align*}L(a,b,\sigma)=f(y_1){\times}f(y_2){\times}f(y_3){\times}f(y_4){\times}f(y_5)\end{align*}$

頑張って式を整理するとこうなる

$\begin{align*}L(\sigma,\varepsilon_i)=\left(\dfrac{1}{\sqrt{2\pi}\sigma}\right)^5\exp\left(-\dfrac{\varepsilon_1^2+\varepsilon_2^2+\varepsilon_3^2+\varepsilon_4^ 2+\varepsilon_5^2}{2\sigma^2}\right)\end{align*}$

やや省略した形ではあるが、これが尤度関数である。

④尤度を最大化する

いよいよ最後に尤度関数を最大化して、パラメーターを求める工程になる。

この $\sigma$ の値を変えてこの尤度関数をグラフにしてみると、常に $\begin{align*}\varepsilon_1^2+\varepsilon_2^2+\varepsilon_3^2+\varepsilon_4^ 2+\varepsilon_5^2\end{align*}$ が最小になるとき、尤度関数Lが最大になることが分かる。